The most reliable method for solving quadratic equations is using the quadratic formula, which is this:

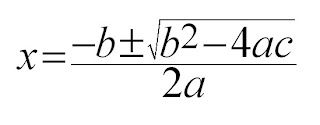
What do a, b, and c stand for? They stand for the following numbers in a quadratic equation:  ax² + bx + c

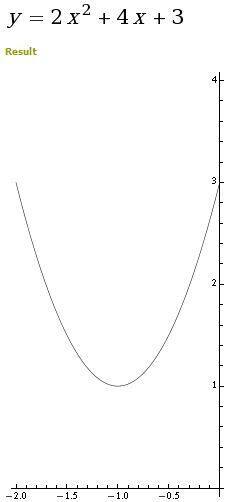
For example, If your quadratic equation was 2x² + 4x + 3, then a = 2, b = 4, c = 3.

Let's use these numbers as an example.

4ac = 4(2)(3) = 8(3) = 24

-4ac = -24

b² = 4² = 16

b² - 4ac = 16 - 24 = -8

?-8 = ???

Ah. We're being asked to find the square root of minus 8. But square roots of negative numbers are imaginary numbers. What this essentially means is we can't solve this equation - therefore there must be no values for x when y=0. Here's proof (notice how the blue line doesn't reach the x-axis):

The Discriminant

The part of the formula we just worked out  (b² - 4ac) is known as the 'discriminant'.

• If the discriminant is a negative number, it means the equation is unsolvable and there are no values for x when y=0.  (Because if the discriminant is a negative number, it won't have a square root, and we can't carry on with the quadratic formula).
• If it's positive, then x has 2 values when y=0. (Because a positive number has 2 possible square roots).
• If the discriminant is zero, then x has just one value. (Because zero has just one square root - zero).

Finding the vertex co-ordinates

The remaining part of the formula can find the x co-ordinate at the vertex of the graph (the vertex is the graph's highest or lowest point):

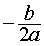
You use this to find the vertex x co-ordinate.

Finding the y co-ordinate at the vertex is easy, just substitute your x value into the original quadratic equation.

Notice that x co-ordinate is independent of the 'c' value. This is because changing the value for c only makes the graph go up or down.

If the vertex lay on the x-axis, the discriminant would be zero. Therefore finding the vertex x co-ordinate (using the formula above) would be the same as using the quadratic formula to get the x value where y = 0 (you would use the formula above then add the discriminant, i.e. zero).

Why is finding the vertex co-ordinates important? Graphs are fairly boring and each has just a few notable features, which exam boards love making you find:

1. the vertex
2. the x co-ordinates where the graph touches the x-axis (if any)
3. the y co-ordinate where the graph touches the y-axis (if any)  - easy to find by substituting 0 for x in the original quadratic equation