Mathematical functions
This will (hopefully) be the first of a series of posts on mathematical functions. The purpose is to help me learn the material to pass an A Level in Mathematics.
Contents
1. Introduction
2. Real-life examples of functions
3. Solving quadratic equations
Introduction
A function is: a variable (called 'y') whose value is completely determined by the value of a second variable (called 'x').
What does this mean?
If you change the value of x, you get a new value for y.
Let's look at an example to make it more clear.
Example: y=x
The simplest example of a function is y = x.
Here, the value of y is always the same as x.
E.g., say x is 3. y would equal 3 too, as y equals x.
Functions are drawn as graphs so that we get something to look at instead of a formula.
Below is the graph for the function y = x.
Notice that the values for x are on the horizontal axis (which is called the 'x-axis') and the values for y on the vertical axis (called the 'y-axis').
Where the x-axis and y-axis meet, x and y both equal 0.
Quadratic equations
When you introduce an x² to the function, it becomes a quadratic equation.
What does this mean?
Essentially, the graph becomes curved instead of being a straight line all the time.
Here's the graph for y = x²

Why is it curved?
Because each time you add 1 to x, y increases by a larger and larger amount.
Look at the following values for x and y to confirm this for youself:
x function y
1 1² = 1
2 2² = 4
3 3² = 9
4 4² = 16
Notice the area of the graph where there are negative x values but postive y values. Why is this?
Because when you square a negative number you get a positive number.
E.g.: -2² = -2 x -2 = 4
Again, here are the x and y values so you can see for youself:
x function y
-1 -1² = 1
-2 -2² = 4
-3 -3² = 9
-4 -4² = 16
Why are quadratic equations so important?
I don't really know yet. They feature heavily in A level Mathematics however!They have x²'s, and the only purpose of a squaring a number is to find the area of a square. At least, that's all I can think of.
Pythagoras' theorem has squared numbers in it: hyp² = opp² + adj². But this is because it involves turning straight lines into squares.
Beyond the quadratic
To summarise so far:
in linear equations, the highest power x is raised to 1 (x¹)
in quadratics, the highest power x is raised to 2 (x²)
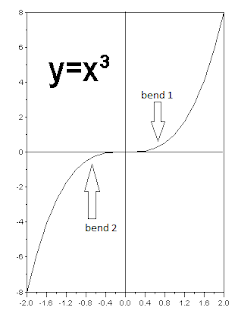
What happens if you introduce a x³? The equation is no longer quadratic. It's called a cubic equation.
Going from quadratic to cubic equations introduces another curve in the graph. Essentially, the number of 'bends' in the graph is equal to the power that x is raised by, then subtracting 1.
in cubic equations, the highest power x is raised to 3 (x³)
in quartic equations, the highest power x is raised to 4 (x?)
Going from quadratic to cubic equations introduces another curve in the graph. Essentially, the number of 'bends' in the graph is equal to the power that x is raised by, then subtracting 1.
E.g. a quadratic has (x)²?¹ = 1 curve.
A linear equation has (x)¹?? = 0 curves.
Let's look at a graph of the equation y = x³:



Leave a comment